INFORMATION

BINARY AND DECIMAL NUMBERS

Binary and decimal numbering systems are commonly used in mathematics, computer science and electrical engineering.

Binary Numbering System (Base 2): In the binary system, numbers are represented using one of two digits: 0 and 1. Each digit is called a bit. For a whole number, the right-most bit has a place value of 2⁰ = 1, the next bit has a place value of 2¹ = 2, then 2² = 4, 2³ = 8, and so on, doubling with each position to the left. For a binary number with a radix point, the place value of the left-most digit in the fractional part is 2^–1, the next bit on the right has a place value 2^–2, and so on.

Decimal Numbering System (Base 10): In the decimal system, numbers are represented using ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Each digit has a place value of 10 raised to a power depending on its position in the number.

BINARY TO DECIMAL CONVERSION

Each binary number has a unique representation in decimal system. Binary to decimal (bin to dec) conversion is the process of converting a binary number into its equivalent decimal representation. To convert a binary number to decimal we multiply each digit by its place value and add the products.

PLACE VALUES OF A BINARY NUMBER

Each place value in a binary number can be represented using an exponential number with a base of 2. The exponent of the ones digit is zero, and it increases by 1 for each digit moved to the left. In other words,

• the place value of the ones digit is 1,
• as we move to the left, the place value is doubled and
• as we move to the right the place value is halved.

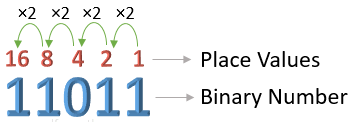
Each digit of the binary number above is marked with its place value. The place value of the ones digit is 1, the next digit's place value is 2, which is twice that of 1, and the subsequent digit's place value is 4, which is twice that of 2, and so on.

The place value of the ones digit is 1, and as we move to the right, the place value halves, resulting in place values in fraction form such as ..., ..., ..., and so on.

BINARY TO DECIMAL CONVERSION EXAMPLES

EXAMPLE:

Find the decimal representation of the binary number 1011₂.

The place values, from left to right, are 8, 4, 2, and 1, respectively. To find the decimal equivalent, we multiply each place value by the corresponding digit and then add the products together.

1011₂ = 1 · 8 + 0 · 4 + 1 · 2 + 1 · 1

= 8 + 2 + 1

= 11

So, the decimal representation of 1011₂ is 11₁₀.

EXAMPLE:

Find the decimal equivalent of the binary number 110.11₂.

The place values of 110.11₂ are shown below.

Multiply those values with the corresponding digits and add the products.

... ... ...

...

...

...

EXAMPLE:

Find the decimal equivalent of the largest 8-digit binary number.

The highest possible value of a binary digit is 1. Therefore, the largest 8-digit binary number is 11111111₂. Its decimal equivalent is:

11111111₂ = 1 · 2⁷ + 1 · 2⁶ + 1 · 2⁵ + 1 · 2⁴ + 1 · 2³ + 1 · 2² + 1 · 2¹ + 1 · 2⁰

= 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1

= 255₁₀

Alternatively, we can find the decimal equivalent of the smallest 9-digit binary number and subtract 1 to reach the result faster. The smallest 9-digit binary number is 100000000₂.

100000000₂ = 2⁸

= 256₁₀

That number is 1 more than the largest 8-digit binary number.

11111111₂ = 256 - 1

= 255₁₀

EXAMPLE:

If 1a001₂ = 2b₁₀, find the sum a + b.

Let's find the decimal equivalent of the binary number 1a001₂.

1a001₂ = 16 + 8 · a + 1

= 17 + 8a

There are only two possible values for a: 0 and 1. If a were 0, the decimal equivalent of this number would be 17₁₀. However, since 2b₁₀ cannot equal 17₁₀, a cannot be 0. Therefore, a = 1. When we calculate the decimal equivalent for this value:

17 + 8 * 1 = 25₁₀

Consequently, b = 5. The sum of the numbers a = 1 and b = 5 is 6.

BINARY TO DECIMAL CONVERSION TABLE

The table below provides the decimal equivalents of the binary numbers up to 100.

WHAT IS BINARY TO DECIMAL CONVERTER?

Binary to decimal converter,

• Computes the decimal equivalent of the entered binary number,
• Describes the solution step by step and
• Illustrates the place values.

HOW TO USE BINARY TO DECIMAL CONVERTER?

You can use binary to decimal converter in two ways.

• USER INPUTS

  

  You can enter a binary number into the input box and then click the 'CONVERT' button. The result and explanations will appear below the calculator.

• RANDOM INPUTS

  

  You can click on the DIE ICON next to the input box to generate a random binary number, which will be automatically entered into the calculator. The result and explanations will then appear below the calculator. You can also create your own examples and practice using this feature.

• CLEARING THE INPUT BOX

  

  To find the decimal equivalent of another binary number, click on the CLEAR button to clear the input box.

• COPYING & DOWNLOADING THE SOLUTION

  • 

    You can copy the generated solution by clicking on the 'Copy Text' link located below the solution panel.

  • 

    You can also download the solution as an image file with a .jpg extension by clicking on the 'Download Solution' link located at the bottom of the solution panel. You can then share the downloaded image file.